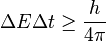Vivimos en una sociedad del riesgo, esta característica diferencia nuestras sociedades actuales y las sociedades industriales, según U. Beck.
Tiempos de incertidumbre. La incertidumbre no es una anomalía, una excepción que haya que erradicar; al contrario, es una variable esencial que debería introducirse en todos los elementos de una educación del s.XXI.
Una educación para la incertidumbre, es una educación donde no hay certezas en gran parte de los elementos, procesos y estructuras que nos rodean. Si tiene sentido verdaderamente aprender a aprender, es porque sabemos de antemano que el presente no tiene asegurado una linealidad y secuencialidad en el futuro, que sí tenía en una sociedad industrial. No hay certeza en qué elementos serán los principales en nuestro itinerario biográfico y profesional; no hay certeza en la dinámica de los procesos económicos, sociales o políticos donde vivimos y estamos; no hay certeza en las estructuras que, por inercia, nos rodean y protegen actualmente: qué tipo de Estado o qué tipo de mercado, qué tipo de sistema educativo o sistema sanitario, son estructuras que acelerarán su dinámica, hasta convertirse en rostros irreconocibles para el sujeto actual. Esa aceleración crecerá. El determinismo que la física cuántica derrumbó en el s.XX, hoy se muestra como un cadáver explicativo de nuestra época. Una educación para la incertidumbre debería interiorizar estas características, significando su inevitabilidad y estrategias.
Una educación para la incertidumbre, es una educación para la hibridación de los elementos, procesos y estructuras que nos rodean. Nuestra sociedad del conocimiento rompe esas dualidades que, tan bien, nos protegían en su oposición teórica y práctica. En forma de preguntas: ¿tiene sentido una organización curricular que divida ciencias y letras? ¿tiene sentido oponer la naturaleza y la cultura, no son procesos ya convergentes y, muchas veces, sintetizados en nuestra cultura/naturaleza tecnologizada? Sí, nuestra globalización compleja es una época híbrida, un tiempo donde lo nuevo no pide permiso a las fronteras de las disciplinas y los géneros.
Una educación para la incertidumbre, es una educación para la flexibilidad del tiempo y el espacio. M. Castells describe cómo las nuevas tecnologías habían y estaban transformando estas nuevas relaciones temporales y espaciales. Cómo esta multiplicidad temporal y espacial va a dibujar nuestras vidas, cómo la red se introduce como modelo de explicación en ámbitos insospechados, es comprender que el tiempo y el espacio están siendo procesos mediados tecnológicamente, con efectos imposibles de predecir.
El principi d'incertesa de Heisenberg
El Principi d'incertesa d'Heisenberg explica que no es pot saber, al mateix temps i amb total precisió, el valor de certs observables com per exemple la posició i el moment d'una partícula. El principi d'incertesa és un dels principis més importants de la mecànica quàntica i va ser formulat per Werner Heisenberg el 1927. També s'anomena principi d'indeterminació de Heisenberg.
Segons Heisenberg, no és possible precisar la posició d'una partícula quàntica ja que aquestes "no tenen una extensió fixa" i, per tant, "no són pas corpuscles localitzats" i no té sentit parlar de quina és la seva posició.
Ve del món de la ciència, però, com sempre, té múltiples aplicacions a la resta de camps. El principi d'incertesa de Heisenberg afirma que, al món microscòpic, l'acció de l'observador altera per si matixa el sistema observat. Manuel Vicent: "Si se aplica al periodismo, una noticia pierde veracidad por el hecho de publicarla".
Introducció a la mesura
En qualsevol mesura que fem sempre tenim associat un error. Aquest error es degut a que fem servir un aparell de mesura i que per tant aquest no és perfecte. Per exemple, si volem mesurar la llargada d'una taula podem fer servir un regle. A aquesta mesura li podem assignar, a grosso modo, un error d'un mil·límetre (si fem servir un regle corrent) donat que és l'error mínim que sabem que podem fer en mesurar la llargada de la taula amb aquest aparell. Si ara volem incrementar la precisió en la nostra mesura podem fer servir un regle més precís. Així i tot tindrem encara associada a la mesura un cert error.
Suposem ara que tenim un conjunt de taules idèntiques entre elles i que mesurem la seva llargada. Si ara dibuixem la frequència de les mesures fetes, veurem que segueixen una certa distribució. Aquesta distribució segueix una distribució gaussiana caracteritzada per un valor mig, la nostra mesura, i una desviació estàndard, que ens diu com de disperses estàn les nostres mesures respecte del valor mig (és una manera d'evaluar l'error fet en les mesures).
Formulació del principi d'incertesa
El principi d'incertesa tracta de la relació entre les desviacions estàndard dels observables (o més intuitivament dels errors al mesurar els observables). Segons aquest, per dues variables conjugades amb desviacions estàndard Δ1 i Δ2 respectivament, no podrem reduir Δ1 més enllà d'un límit sense incrementar Δ2 i viceversa. Exemples de variables conjugades són el moment i la posició, i l'energia i el temps.
Veiem un exemple. Si preparem primer moltes copies de un sistema en un estat quàntic determinat i després mesurem la posició i el moment d'aquestes còpies, llavors trobarem que els valors d'aquestes variaran d'acord a l'anomenada distribució de probabilitats. Ara podem mesurar la desviació estàndard Δx de la posició i la desviació estàndard Δp de les mides del moment. Si ho fem, el principi d'incertesa ens dóna una relació entre aquestes dues i que matemàticament s'expressa com:
on h és la Constant de Planck, i π és la constant d'Arquímedes. Com dèiem abans: no podem disminuir tan com volem Δx sense incrementar necessariament Δp i viceversa.
A la mecànica quàntica aquest és un postulat fonamental i no es refereix únicament a l'error que fem al mesurar, sinó a un error intrínsec que no podem superar. Per l'energia i el temps:
Els inicis de la mecànica quàntica i el principi d'incertesa
A principis del segle XX la física va conèixer dues grans revolucions; una amb el naixement de la teoria de la relativitat i l'altra amb el naixement de la mecànica quàntica. Un fet que va marcar la mecànica quàntica, a diferència de la teoria de la relativitat, formulada bàsicament per Albert Einstein, és que va tenir moltes contribucions importants de diferents físics, entre ells el mateix Albert Einstein. Això va fer que en sorgissin una sèrie d'interpretacions diferents. La més acceptada comunament és la interpretació de Copenhaguen, formulada entre d'altres per Niels Bohr i Werner Heisenberg. Aquesta interpretació creu en la veracitat del principi d'incertesa de Heisenberg.
Altres físics molt importants, com Albert Einstein, Erwin Schrödinger o Louis de Broglie, pensaven diferent i malgrat haver fet moltes i importants aportacions a la mecànica quàntica, avui formulada segons la interpretació de Copenhaguen, no hi estaven d'acord. Un exemple d'això és el famós article Einstein-Podolsky-Rosen, conegut com EPR (vegeu les referències), on es qüestiona que la mecànica quàntica sigui una teoria completa i refuten, per tant, el principi d'incertesa.
En aquest marc, on els millors físics del segle XX es van involucrar en un cantó o l'altre, Einstein i Bohr van mantenir un debat molt important, on els anomenats gedanke Experimente (experiments mentals) van jugar un rol molt important. Aquests experiments mentals intentaven refutar, arribant a absurds o paradoxes, o donar suport a la mecànica quàntica. És en aquest context que Einstein va dir la seva famosa frase: "no crec que Déu decidís jugar als daus amb l'univers". La rèplica de Bohr va ser: "Einstein, no li diguis a Déu el que ha de fer".
Intents de refutar el principi d'incertesa
Amb el temps, el debat sobre la mecànica quàntica va anar perdent intensitat, malgrat que, en certa manera, encara és vigent. Una aproximació diferent, per mirar de superar la visió no determinista de la mecànica quàntica tradicional, és la inclusió de variables ocultes. Una teoria d'aquest estil proposa afegir una serie de variables, fins ara no mesurables, i que faria que la mecànica quàntica actual fos només una visió estadística d'una teoria més complerta. Sembla clar que fins i tot una teoria de variables ocultes ha d'incloure la no localitat observada a la mecànica quàntica. El físic von Neumann va creure demostrar amb un teorema que una teoria de variables ocultes no era possible si aquesta havia de reproduir els resultats, realment excel·lents, de la mecànica quàntica. Més tard es va veure que el teorema només descarta un tipus determinat de teoria de variables ocultes.
Una exemple de teoria de variables ocultes, no local però determinista, és la desenvolupada per David Bohm el 1952. Aquesta és coneguda com mecànica de Bohm i es basa en una reinterpretació de l'equació de Schrödinger en l'equació de Hamilton-Hacobi, ja coneguda a la mecànica clàssica, i que inclou la idea ja formulada per de Broglie de les ones pilot.
En conclusió, és pot dir que, si bé el principi d'incertesa va en contra de l'experiència quotidiana i que alguns físics han mirat de trobar una teoria que la substitueixi, no s'ha trobat cap experiment que el refuti definitivament. També és cert que no s'ha demostrat definitivament la impossibilitat d'una teoria de variables ocultes (sí han estat descartades algunes de les possibles teories). Així doncs el debat està encara obert malgrat que ha perdut molta intensitat i que hi han pocs físics que es preguntin avui dia sobre aquesta qüestió.